pacman::p_load(sf, spdep, tmap, tidyverse)Hands-on Exercise 2: Local Measures of Spatial Autocorrelation
Overview
In this hands-on exercise, I learned how to compute Global and Local Measure of Spatial Autocorrelation (GLSA) by using spdep package.
import geospatial data using appropriate function(s) of sf package,
import csv file using appropriate function of readr package,
perform relational join using appropriate join function of dplyr package,
compute Global Spatial Autocorrelation (GSA) statistics by using appropriate functions of spdep package,
plot Moran scatterplot,
compute and plot spatial correlogram using appropriate function of spdep package.
compute Local Indicator of Spatial Association (LISA) statistics for detecting clusters and outliers by using appropriate functions spdep package;
compute Getis-Ord’s Gi-statistics for detecting hot spot or/and cold spot area by using appropriate functions of spdep package; and
to visualise the analysis output by using tmap package.
Study Area & Data
Hunan province administrative boundary layer at county level. This is a geospatial data set in ESRI shapefile format.
Hunan_2012.csv: This csv file contains selected Hunan’s local development indicators in 2012.
Getting Started
The code chunk below installs and load sf and tidyverse packages into R environment
Getting the Data Into R Environment
Bring geospatial data (ESRI shapefile) and its associated attribute (csv) into R environment.
Import shapefile into R environment
st_read() is used to import Hunan shapefile into R. The imported shapefile will be simple features Object of sf.
hunan <- st_read(dsn = "data/geospatial",
layer = "Hunan")Reading layer `Hunan' from data source
`C:\lnealicia\ISSS624\Handson_ex02\data\geospatial' using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84Import csv file into r environment
Import Hunan_2012.csv into R using read_csv(), the output is a R dataframe class.
hunan2012 <- read_csv("data/aspatial/Hunan_2012.csv")Relational Join
Update the attribute table of hunan’s SpatialPolygonsDataFrame with attribute fields of hunan2012 dataframe via leftjoin() of dplyr package.
hunan <- left_join(hunan,hunan2012)%>%
select(1:4, 7, 15)Visualising Regional Development Indicator
Prepare a basemap and a choropleth map showing the distribution of GDPPC 2012 by using qtm() of tmap package.
equal <- tm_shape(hunan) +
tm_fill("GDPPC",
n = 5,
style = "equal") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Equal interval classification")
quantile <- tm_shape(hunan) +
tm_fill("GDPPC",
n = 5,
style = "quantile") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Equal quantile classification")
tmap_arrange(equal,
quantile,
asp=1,
ncol=2)
Global Spatial Autocorrelation
Compute global spatial autocorrelation statistics and to perform spatial complete randomness test for global spatial autocorrelation.
Computing Contiguity Spatial Weights
Construct a spatial weights of the study area to compute the global spatial autocorrelation statistics
poly2nb() of spdep package is used to compute contiguity weight matrices for the study area.
wm_q <- poly2nb(hunan, queen=TRUE)
summary(wm_q)Neighbour list object:
Number of regions: 88
Number of nonzero links: 448
Percentage nonzero weights: 5.785124
Average number of links: 5.090909
Link number distribution:
1 2 3 4 5 6 7 8 9 11
2 2 12 16 24 14 11 4 2 1
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 linksThe summary report above shows that there are 88 area units in Hunan. The most connected area unit has 11 neighbours. There are two area units with only one neighbours.
Row-standardised weights matrix
Assign weights to each neighboring polygon. Below, each neighboring polygon will be assigned equal weight (style=“W”).
This is done via assigning the fraction 1/ (# of neighbours) to each neighbouring country then adding up the weighted income values.
Drawback: Polygons along the edges of the study area will base their lagged values on fewer polygons, thus potentially over- or under-estimating the true nature of the spatial autocorrelation in the data.
rswm_q <- nb2listw(wm_q, style="W", zero.policy = TRUE)
rswm_qCharacteristics of weights list object:
Neighbour list object:
Number of regions: 88
Number of nonzero links: 448
Percentage nonzero weights: 5.785124
Average number of links: 5.090909
Weights style: W
Weights constants summary:
n nn S0 S1 S2
W 88 7744 88 37.86334 365.9147The input of nb2listw() must be an object of class nb. The syntax of the function has two major arguments, namely style and zero.poly.
Global Spatial Autocorrelation: Moran’s I
Perform Moran’s I statistics testing by using moran.test() of spdep.
moran.test(hunan$GDPPC,
listw=rswm_q,
zero.policy = TRUE,
na.action=na.omit)
Moran I test under randomisation
data: hunan$GDPPC
weights: rswm_q
Moran I statistic standard deviate = 4.7351, p-value = 1.095e-06
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.300749970 -0.011494253 0.004348351 Conclusion: Given the small p-value < 0.05, we reject the null hypothesis of spatial randomness. Therefore, there is strong evidence that the variable hunan$GDPPC exhibits positive spatial autocorrelation in relation to the specified spatial weights. Regions with similar values of hunan$GDPPC are clustered together, suggesting a spatial pattern in the distribution of this variable.
Computing Monte Carlo Moran’s I
Perform permutation test for Moran’s I statistic by using moran.mc() of spdep. A total of 1000 simulation will be performed.
set.seed(1234)
bperm= moran.mc(hunan$GDPPC,
listw=rswm_q,
nsim=999,
zero.policy = TRUE,
na.action=na.omit)
bperm
Monte-Carlo simulation of Moran I
data: hunan$GDPPC
weights: rswm_q
number of simulations + 1: 1000
statistic = 0.30075, observed rank = 1000, p-value = 0.001
alternative hypothesis: greaterConclusion: Given the small p-value < 0.05, we reject the null hypothesis of spatial randomness. Therefore, there is strong evidence that the variable hunan$GDPPC exhibits positive spatial autocorrelation in relation to the specified spatial weights. Regions with similar values of hunan$GDPPC are clustered together, suggesting a spatial pattern in the distribution of this variable.
Visualising Monte Carlo Moran’s I
Plotting the distribution of the statistical values as a histogram
mean(bperm$res[1:999])[1] -0.01504572var(bperm$res[1:999])[1] 0.004371574summary(bperm$res[1:999]) Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.18339 -0.06168 -0.02125 -0.01505 0.02611 0.27593 hist(bperm$res,
freq=TRUE,
breaks=20,
xlab="Simulated Moran's I")
abline(v=0,
col="red") 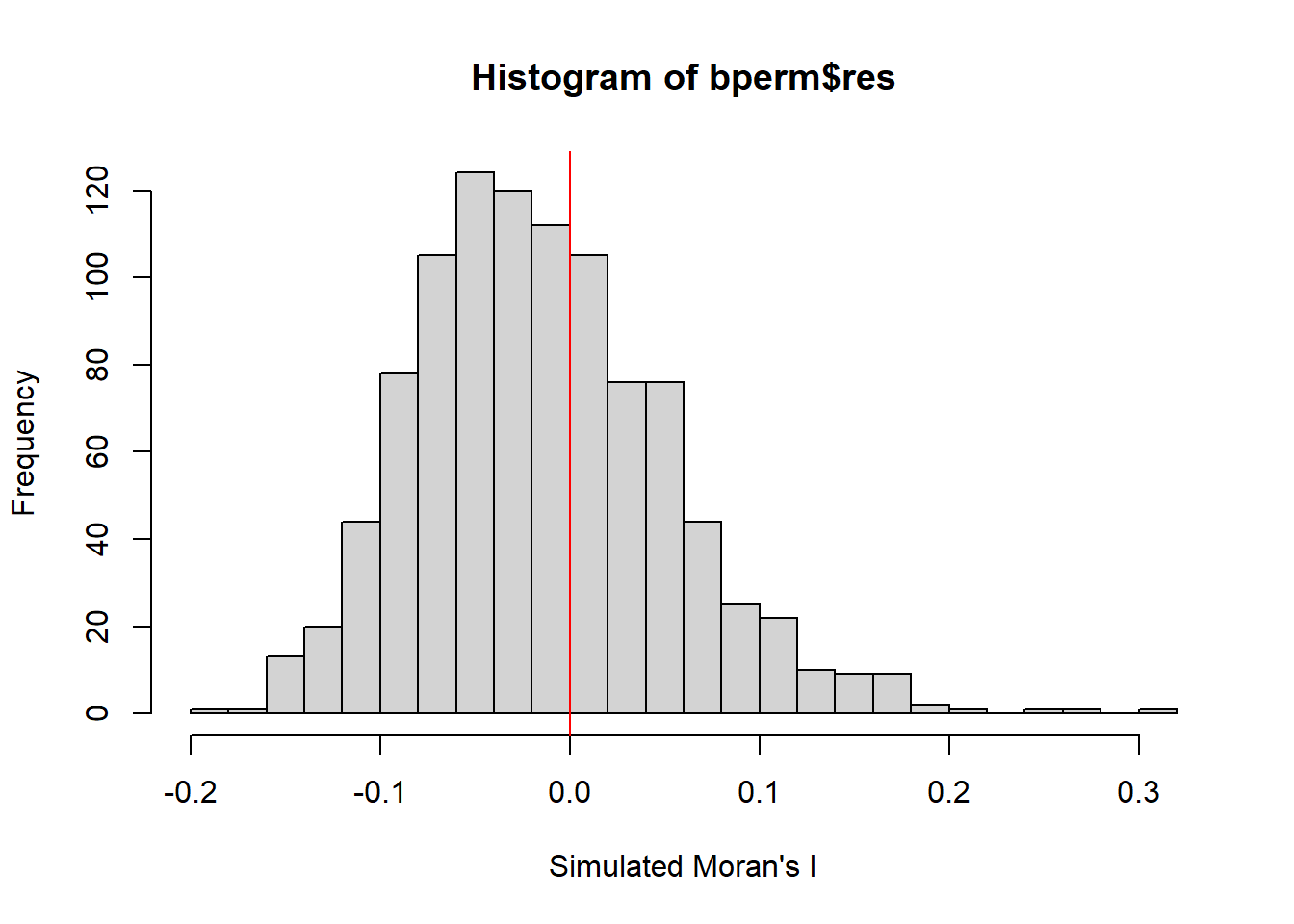
Conclusion: The statistical observation suggests that the observed spatial autocorrelation in the variable hunan$GDPPC is unlikely to be due to random chance, as indicated by its position (red line) in the distribution of simulated Moran I values.
Global Spatial Autocorrelation: Geary’s
Perform Geary’s c statistics testing by using appropriate functions of spdep package
Geary’s C test
geary.test(hunan$GDPPC, listw=rswm_q)
Geary C test under randomisation
data: hunan$GDPPC
weights: rswm_q
Geary C statistic standard deviate = 3.6108, p-value = 0.0001526
alternative hypothesis: Expectation greater than statistic
sample estimates:
Geary C statistic Expectation Variance
0.6907223 1.0000000 0.0073364 Conclusion: Given that the p-value is <0.05, we reject the null hypothesis of syatial randomness. The small p-value indicates that the observed Geary C statistic is statistically significant, providing evidence that there is positive spatial autocorrelation in the variable hunan$GDPPC with respect to the specified spatial weights (rswm_q). The spatial pattern observed is unlikely to have occurred by random chance alone.
Computing Monte Carlo Geary’s C
Performs permutation test for Geary’s C statistic by using geary.mc() of spdep.
set.seed(1234)
bperm=geary.mc(hunan$GDPPC,
listw=rswm_q,
nsim=999)
bperm
Monte-Carlo simulation of Geary C
data: hunan$GDPPC
weights: rswm_q
number of simulations + 1: 1000
statistic = 0.69072, observed rank = 1, p-value = 0.001
alternative hypothesis: greaterConclusion: Given that the p-value is <0.05, we reject the null hypothesis of syatial randomness. The small p-value indicates that the observed Geary C statistic is statistically significant, providing evidence that there is positive spatial autocorrelation in the variable hunan$GDPPC with respect to the specified spatial weights (rswm_q). The spatial pattern observed is unlikely to have occurred by random chance alone.
Visualising the Monte Carlo Geary’s C
Plot a histogram to reveal the distribution of the simulated values
mean(bperm$res[1:999])[1] 1.004402var(bperm$res[1:999])[1] 0.007436493summary(bperm$res[1:999]) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.7142 0.9502 1.0052 1.0044 1.0595 1.2722 hist(bperm$res, freq=TRUE, breaks=20, xlab="Simulated Geary c")
abline(v=1, col="red") 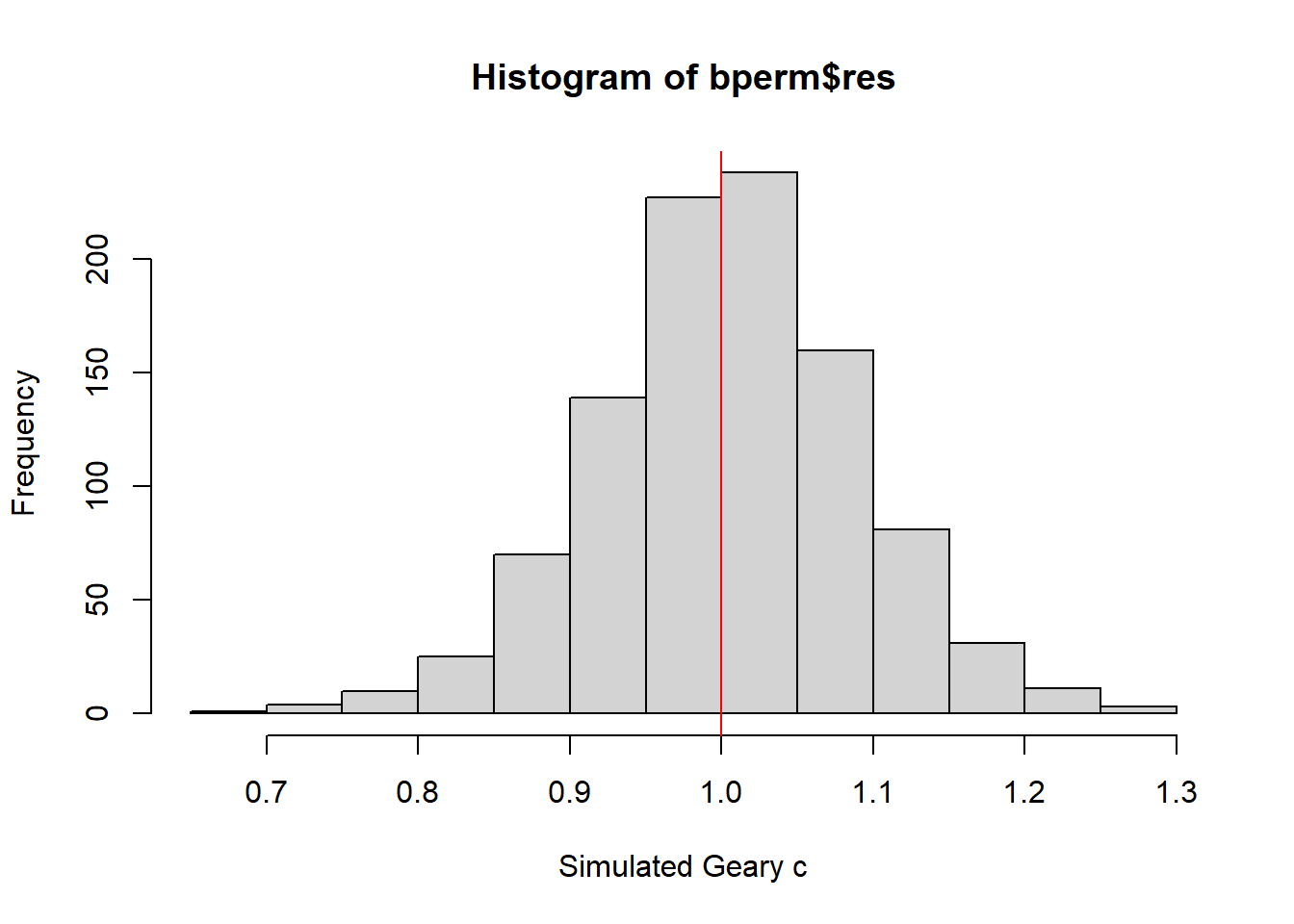
Conclusion: The statistical observation suggests that the observed spatial autocorrelation in the variable hunan$GDPPC is unlikely to be due to random chance, as indicated by its position (red line) in the distribution of simulated Moran I values.
Spatial Correlogram
Spatial correlograms show how correlated are pairs of spatial observations when you increase the distance (lag) between them - they are plots of some index of autocorrelation (Moran’s I or Geary’s c) against distance. Useful as an exploratory and descriptive tool.
Compute Moran’s I correlogram
sp.correlogram() of spdep package is used to compute a 6-lag spatial correlogram of GDPPC. The global spatial autocorrelation used in Moran’s I. The plot() of base Graph is then used to plot the output.
MI_corr <- sp.correlogram(wm_q,
hunan$GDPPC,
order=6,
method="I",
style="W")
plot(MI_corr)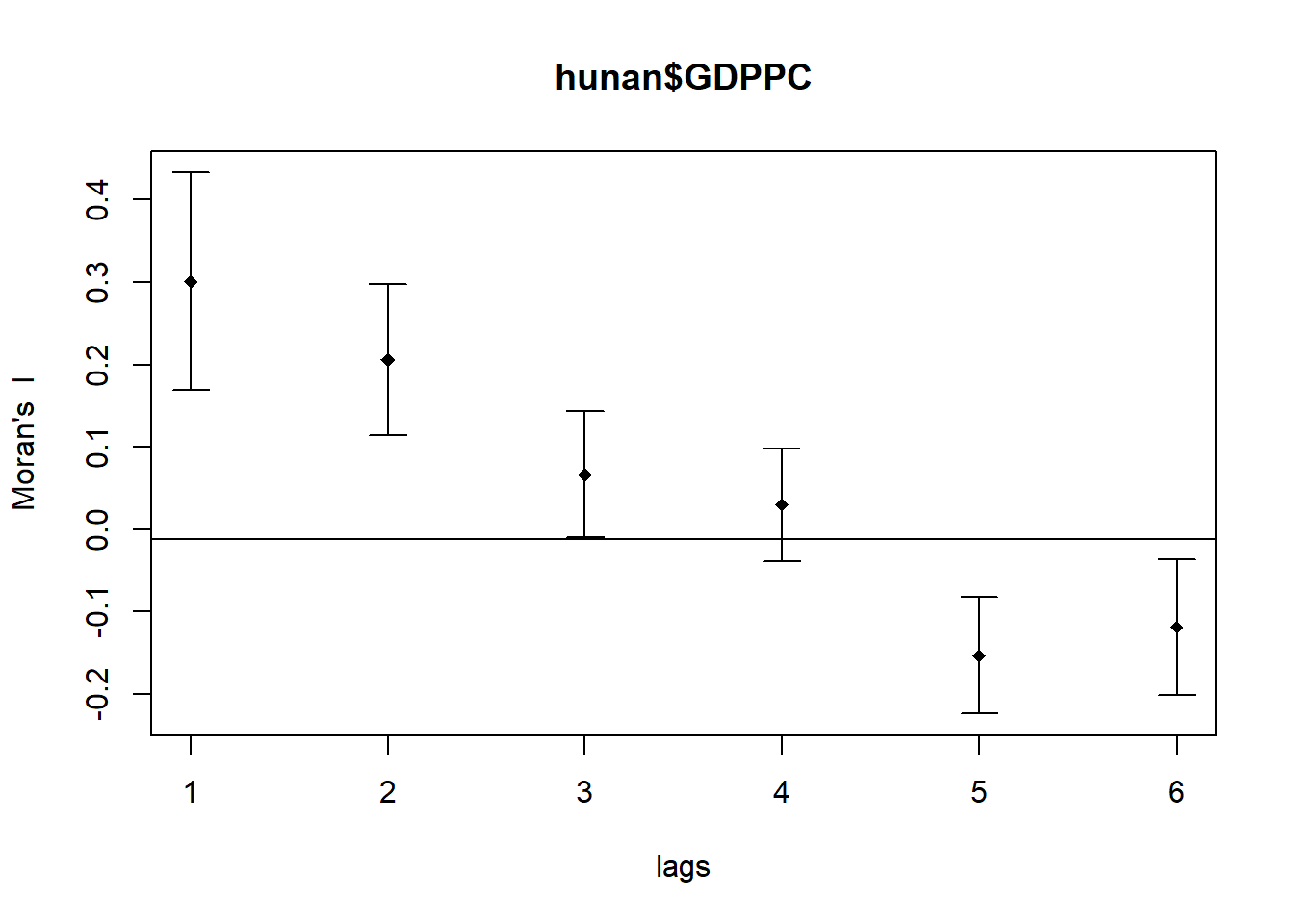
Note: Output plot may not provide complete interpretation, since not all autocorrelation values are statistically significant. Thus, it is important to examine the full analysis report by printing out the analysis results.
print(MI_corr)Spatial correlogram for hunan$GDPPC
method: Moran's I
estimate expectation variance standard deviate Pr(I) two sided
1 (88) 0.3007500 -0.0114943 0.0043484 4.7351 2.189e-06 ***
2 (88) 0.2060084 -0.0114943 0.0020962 4.7505 2.029e-06 ***
3 (88) 0.0668273 -0.0114943 0.0014602 2.0496 0.040400 *
4 (88) 0.0299470 -0.0114943 0.0011717 1.2107 0.226015
5 (88) -0.1530471 -0.0114943 0.0012440 -4.0134 5.984e-05 ***
6 (88) -0.1187070 -0.0114943 0.0016791 -2.6164 0.008886 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The spatial correlogram suggests that there is positive spatial autocorrelation in the variable hunan$GDPPC across different distance classes, and this autocorrelation is statistically significant. The pattern is not likely to be due to random chance alone.
Compute Geary’s C correlogram and plot
sp.correlogram() of spdep package is used to compute a 6-lag spatial correlogram of GDPPC. The global spatial autocorrelation used in Geary’s C. The plot() of base Graph is then used to plot the output.
GC_corr <- sp.correlogram(wm_q,
hunan$GDPPC,
order=6,
method="C",
style="W")
plot(GC_corr)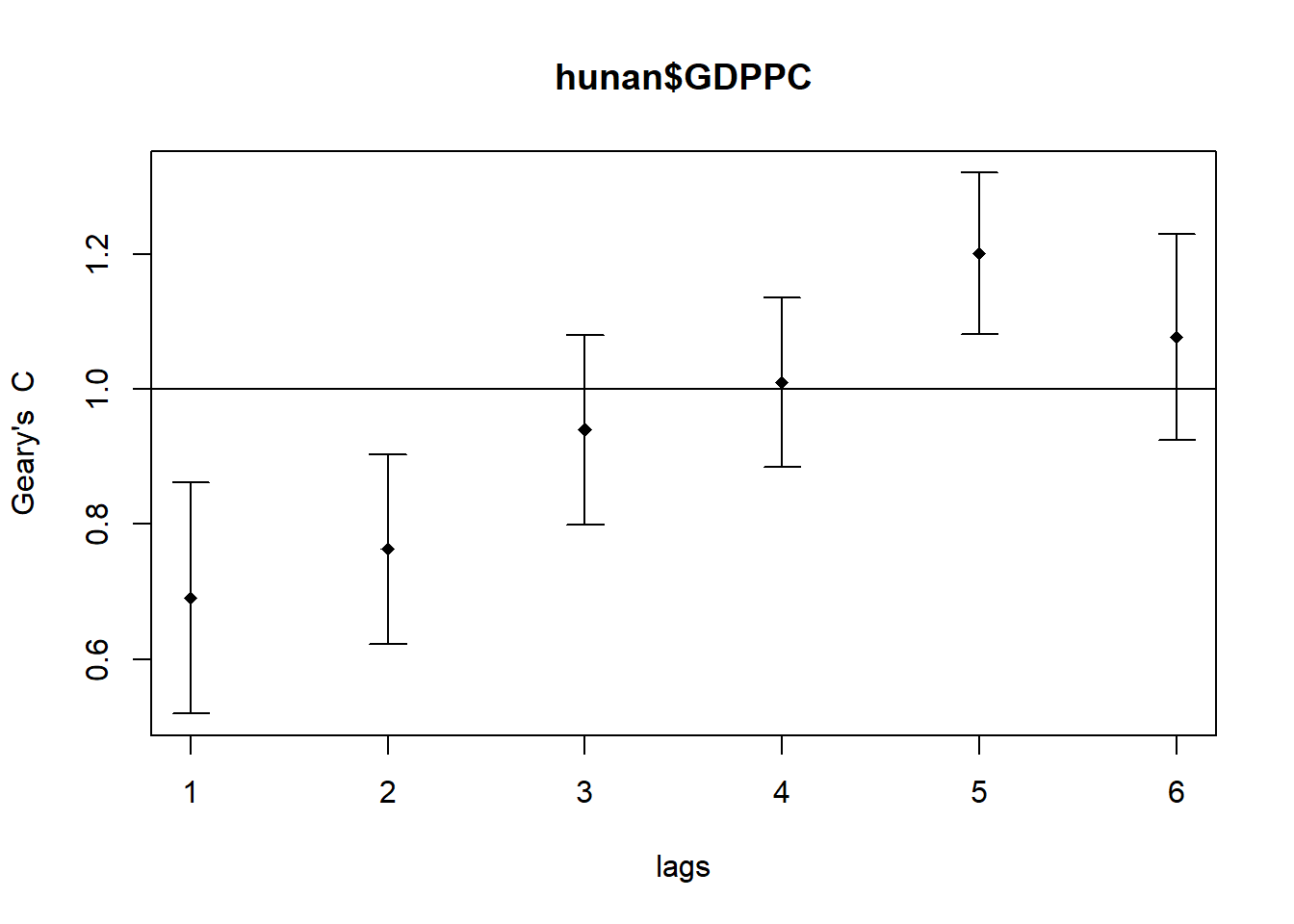
print(GC_corr)Spatial correlogram for hunan$GDPPC
method: Geary's C
estimate expectation variance standard deviate Pr(I) two sided
1 (88) 0.6907223 1.0000000 0.0073364 -3.6108 0.0003052 ***
2 (88) 0.7630197 1.0000000 0.0049126 -3.3811 0.0007220 ***
3 (88) 0.9397299 1.0000000 0.0049005 -0.8610 0.3892612
4 (88) 1.0098462 1.0000000 0.0039631 0.1564 0.8757128
5 (88) 1.2008204 1.0000000 0.0035568 3.3673 0.0007592 ***
6 (88) 1.0773386 1.0000000 0.0058042 1.0151 0.3100407
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1